The derivative of f(x) = c where c is a constant.
f '(x) = 0
Example :
f(x) = 5 , then f '(x) = 0
2 - Derivative of a power function.
The derivative of f(x) = x^n where n is a constant real number.
f '(x) = n x ^(n- 1)
Example :
f(x) = x^7
then,
f '(x) = 7 x^(7-1)
= 7x^6
3 - Derivative of the sum of functions
The derivative of f(x) = g(x) + h(x) is given by
f '(x) = g '(x) + h '(x)
f(x) = 3x^4 + 2x
let g(x) = 3x^4 and h(x) = 2x
then,
f '(x) = g '(x) + h '(x)
= 12x^3 + 2
4 - Derivative of the difference of functions.
The derivative of f(x) = g(x) - h(x) is given by
f '(x) = g '(x) - h '(x)
Example:
f(x) = 5x - x^-2
let g(x) = 5x and h(x) = x^-2
then,
f '(x) = g '(x) - h '(x)
= 5 -(-2x^-3)
= 5 + 2^-3
= 5 + 2^-3
f(x) = (2x^3 + 5)^4
let a = 2, k = 4 and n = 3
thus,
f'(x) = kanx^(n-1)(ax^n + b)^(k-1)
= 4(2)(3)x^2(2x^3 + 5)^3
= 24x^2 (2x^3 + 5)^3
6 - Derivative of the product of two functions
The derivative of f(x) = g(x) h(x) is given by
f '(x) = g(x) h '(x) + h(x) g '(x)
Example:
7 - Derivative of the quotient of two functions
Example :

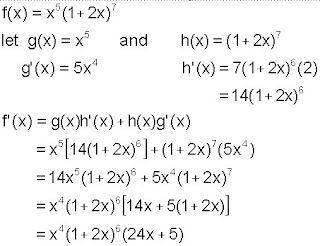


No comments:
Post a Comment